¡Esta es una revisión vieja del documento!
Tabla de Contenidos
Curvas características
Las curvas características corresponden a la probabilidad condicional de elegir una determinada opción de respuesta a una pregunta en función del nivel de conocimiento del alumno. Es lógico suponer que la probabilidad asociada a una respuesta correcta a una pregunta crece al aumentar el nivel de conocimiento.
Modelos politómicos y dicotómicos
Desde el punto de vista del número de opciones de respuesta a una pregunta los modelos de la TRI pueden ser politómicos o dicotómicos. Los modelos politómicos utilizan curvas características distintas para cada una de las posibles respuestas a una pregunta, considerando como tales la selección de una de las opciones y añadiendo tambien la opción de no responder, es decir, dejar la respuesta en blanco.
Por el contrario se llaman modelos dicotómicos a los modelos que solo usan una curva característica asociada a la respuesta correcta, asumiendo que cualquier otra opción de respuesta es incorrecta y su probabilidad es la complementaria a 1.
Modelos no-paramétricos
En el caso más general, puesto que Siette funciona de manera discreta las curvas características corresponden a tablas de probabilidades condicionadas. Por defecto Siette utiliza un modelo politómico.
Por ejemplo, supongamos que en la asignatura se han definido 5 niveles de conocimiento, y supongamos una preguntas de múltiple opción y respuesta única con tres opciones de respuesta, la primera de ellas correcta y las otras dos incorrectas. Para este ítem Siette almacenaría la siguiente tabla de probabilidad condicionada:
| $\theta=\theta_E$ | $\theta=\theta_D$ | $\theta=\theta_C$ | $\theta=\theta_B$ | $\theta=\theta_A$ | |
|---|---|---|---|---|---|
| $u=u_{correcta}$ | 0,274 | 0,452 | 0,625 | 0,789 | 0,911 |
| $u=u_{incorrecta_1}$ | 0,290 | 0,137 | 0,187 | 0,100 | 0,045 |
| $u=u_{incorrecta_2}$ | 0,290 | 0,183 | 0,150 | 0,067 | 0,022 |
| $u=u_{en blanco}$ | 0,145 | 0,228 | 0,038 | 0,034 | 0,022 |
y análogamente para el resto de los ítems. Aplicando la fórmula de Bayes se podrán calcular las probabilidades a posteiori de cada uno de estas clases ($\theta_E ... \theta_A$) según las respuestas de los alumnos a cada uno de los ítems.
En el caso de aplicar un modelo dicotómico podría usarse la tabla
| $\theta=\theta_E$ | $\theta=\theta_D$ | $\theta=\theta_C$ | $\theta=\theta_B$ | $\theta=\theta_A$ | |
|---|---|---|---|---|---|
| $u=u_{correcta}$ | 0,274 | 0,452 | 0,625 | 0,789 | 0,911 |
| $u=u_{correcta}$ | 0,726 | 0,548 | 0,375 | 0,202 | 0,089 |
o simplemente repartir de forma equitativa la probabilidad entre las respuesta incorrectas:
| $\theta=\theta_E$ | $\theta=\theta_D$ | $\theta=\theta_C$ | $\theta=\theta_B$ | $\theta=\theta_A$ | |
|---|---|---|---|---|---|
| $u=u_{correcta}$ | 0,274 | 0,452 | 0,625 | 0,789 | 0,911 |
| $u=u_{incorrecta_1}$ | 0,242 | 0,183 | 0,125 | 0,067 | 0,030 |
| $u=u_{incorrecta_2}$ | 0,242 | 0,183 | 0,125 | 0,067 | 0,030 |
| $u=u_{en blanco}$ | 0,242 | 0,183 | 0,125 | 0,067 | 0,030 |
lo que en la práctica produce los mismos resultados dado que la forma de las curvas es homotética y finalmente se procede a su normalización.
Modelos paramétricos
La teoría de respuesta al ítem clásica se basa en establecer modelos contínuos en donde una variable $\theta$ toma valores en el intervalo real $[-\infty,+\infty]$. El modelo mas simple es el modelo dicotómico en el que cada para cada una de las preguntas se consideran solamente dos casos: respuesta correcta o incorrecta (considerando también la respuesta en blanco como respuesta incorrecta). Los modelos mas comunes se basan en funciones características basadas en la función logística con uno, dos o tres parámetros:
Modelo de Rasch (1PL)
El caso mas simple se basa en suponer que la probabilidad condicionada o curva característica de la respuesta correcta a una pregunta i-esima viene dada por la función logística: $$p_i(\theta) = \frac{1}{1+e^{-Da(\theta-b_i)}}$$
en donde $p_i(\theta)$ es la probabilidad de que un alumno con nivel de conocimiento $\theta$ conteste correctamente a la pregunta i-esima. $b_i$ es un parámetro denominado “dificultad” variable para cada ítem; $a$ es un parámetro denominado “discriminación” que es igual para todos los ítems y $D$ es una constante cuyo valor es 1,702 que hace que la función logística tenga un mayor parecido con la función de distribución (probabilidad acumulada) de la normal $N(0,1)$.
El parámetro $b_i$ corresponde al nivel de conocimiento para el cual es igualmente probable que la respuesta sea correcta o incorrecta. El parámetro $a$ es proporcional a la máxima pendiente de la curva, que se produce precisamente para el valor $\theta=b_i$.
Modelo 2PL
En este caso se asume que las curvas características vienen dadas por dos parámetros para cada pregunta, es decir, que el parámetro $a_i$ puede ser diferente para cada pregunta: $$p_i(\theta) = \frac{1}{1+e^{-Da_i(\theta-b_i)}}$$
Modelo 3PL
En este caso se añade a la curva característica de cada pregunta un tercer parámetro $c_i$ denominado “adivinanza”, que representa la probabilidad de que un alumno sin ningún conocimiento del tema responda correctamente a la pregunta por azar: $$p_i(\theta) = c_i + (1-c_i)\frac{1}{1+e^{-Da_i(\theta-b_i)}}$$
Modelo 4PL
Es un modelo no estandar que introduce Siette, añadiendo un cuarto parámetro $d_i$ llamado “distracción”, que representa la probabilidad de que un alumno, aunque tenga un conocimiento completo del tema, responda incorrectamente debido a cualquier factor fortuito o imprevisto (por ejemplo se salte una pregunta sin querer, o se confunda al seleccionar la respuesta en el interfaz de respuesta). En este caso la curva característica sería $$p_i(\theta) = c_i + (1-c_i-d_i)\frac{1}{1+e^{-Da_i(\theta-b_i)}}$$ El mínimo de esta función es $c_i$ y máximo $1-d_i$
Interpretación de los parámetros
Dificultad
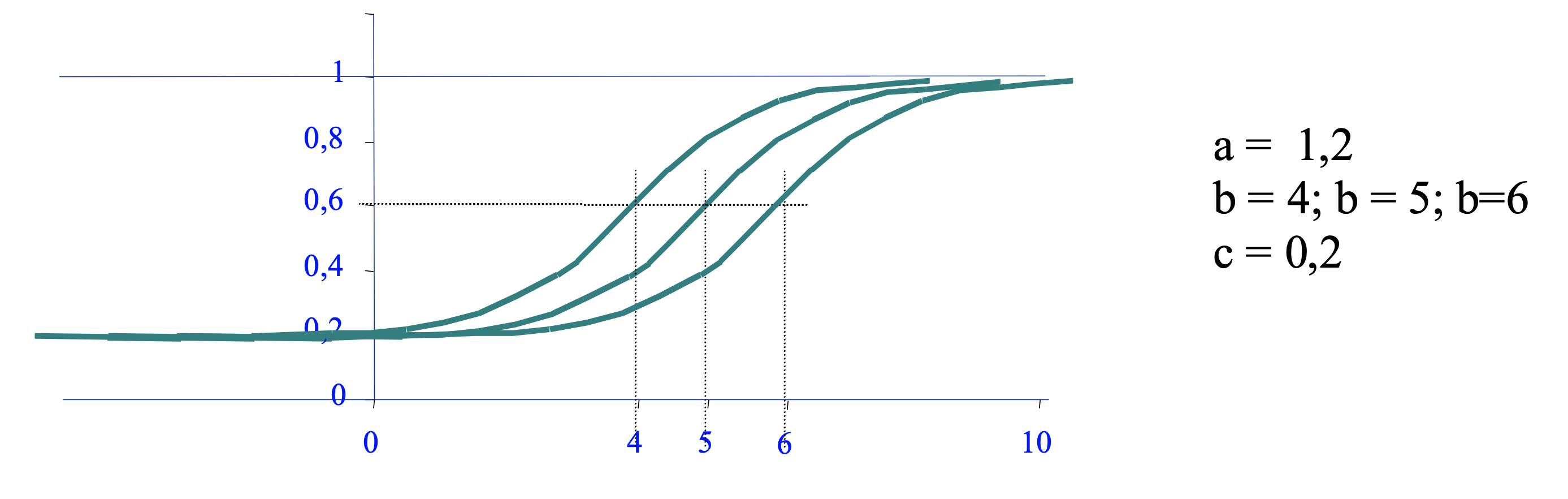
El parámetro $b_i$ se corresponde con la noción intuitiva de “dificultad de una pregunta”. Una preguntas mas difícil tendrá un parámetro $b_i$ mas alto. Al aumentar este parámetro la curva característica se desplaza hacia la derecha, y al disminuir, hacia la izquierda
En el modelo de 1PL, el valor de $\theta = b_i$ coincide con el punto de inflexión de la curva en el que el valor de la probabilidad es exactamente $p(\theta=b_i)=0,5$. En el caso del modelo de 3PL, el valor en $\theta = b_i$ coincide con el punto de inflexión, pero el valor de la probabilidad es $p(\theta=b_i)=c_i+(1-c_i)/2$
Discriminación
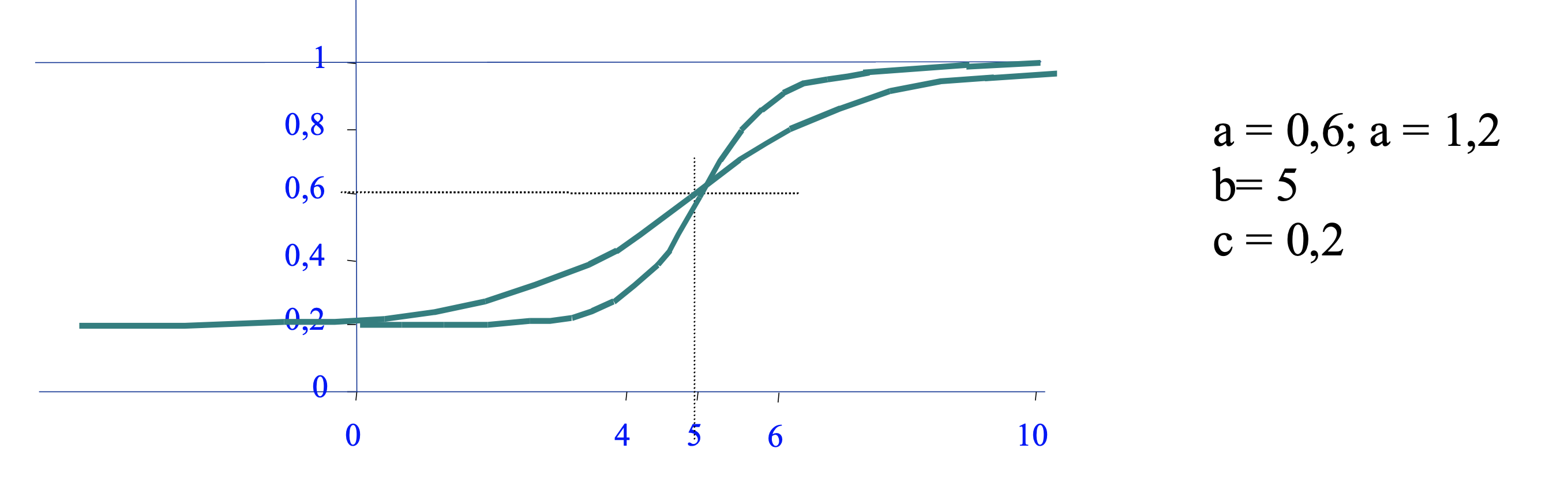
El parámetro $a_i$ modifica la pendiente de la curva. Cuanto mayor sea $a_i$ mayior será la pendiente de la curva en todos los puntos, y especialmente en el punto de inflexión para el que se produce la pendiente máxima.
Este parámetro se llama “factor de discriminación” porque al ser mayor indica que la respuesta a esta pregunta es capaz de discernir con mayor facilidad entre un alumno con conocimiento mayor o menor que el nivel de dificultad $b_i$. Cuando el parámetro $a_i$ es pequeño, la curva característica se aplana, tiene una pendiente pequeña y las probabilidades de respuesta correcta no dependen tanto del nivel de conocimientos del alumno, es decir, la pregunta no discrimina bien.