Tabla de Contenidos
Curvas características
Las curvas características corresponden a la probabilidad condicional de elegir una determinada opción de respuesta a una pregunta en función del nivel de conocimiento del alumno. Es lógico suponer que la probabilidad asociada a una respuesta correcta a una pregunta crece al aumentar el nivel de conocimiento.
Los valores de estas probabilidades condicionadas se obtienen a partir de los resultados de una muestra suficientemente grande de alumnos que hayan realizado el test con anterioridad, mediante un proceso denominado calibración.
Modelos politómicos y dicotómicos
Desde el punto de vista del número de opciones de respuesta a una pregunta los modelos de la TRI pueden ser politómicos o dicotómicos. Los modelos politómicos utilizan curvas características distintas para cada una de las posibles respuestas a una pregunta, considerando como tales la selección de una de las opciones y añadiendo tambien la opción de no responder, es decir, dejar la respuesta en blanco.
Por el contrario se llaman modelos dicotómicos a los modelos que solo usan una curva característica asociada a la respuesta correcta, asumiendo que cualquier otra opción de respuesta es incorrecta y su probabilidad es la complementaria a 1.
Modelos no-paramétricos
En el caso más general, puesto que Siette funciona de manera discreta las curvas características corresponden a tablas de probabilidades condicionadas. Por defecto Siette utiliza un modelo politómico.
Por ejemplo, supongamos que en la asignatura se han definido 5 niveles de conocimiento, y supongamos una preguntas de múltiple opción y respuesta única con tres opciones de respuesta, la primera de ellas correcta y las otras dos incorrectas. Sea $u$ la respuesta del alumno, que puede elegir una cualquiera de estas opciones o dejar la pregunta en blanco; y $\theta$ su nivel de conocimiento. Para este ítem, Siette almacenaría la siguiente tabla de probabilidad condicionada:
| $\theta=\theta_E$ | $\theta=\theta_D$ | $\theta=\theta_C$ | $\theta=\theta_B$ | $\theta=\theta_A$ | |
|---|---|---|---|---|---|
| $u=u_{correcta}$ | 0,274 | 0,452 | 0,625 | 0,789 | 0,911 |
| $u=u_{incorrecta_1}$ | 0,290 | 0,137 | 0,187 | 0,100 | 0,045 |
| $u=u_{incorrecta_2}$ | 0,290 | 0,183 | 0,150 | 0,067 | 0,022 |
| $u=u_{en blanco}$ | 0,145 | 0,228 | 0,038 | 0,034 | 0,022 |
y análogamente para el resto de los ítems. Aplicando la fórmula de Bayes se podrán calcular las probabilidades a posteiori de cada uno de estas clases ($\theta_E ... \theta_A$) según las respuestas de los alumnos a cada uno de los ítems.
En el caso de aplicar un modelo dicotómico podría usarse la tabla
| $\theta=\theta_E$ | $\theta=\theta_D$ | $\theta=\theta_C$ | $\theta=\theta_B$ | $\theta=\theta_A$ | |
|---|---|---|---|---|---|
| $u=u_{correcta}$ | 0,274 | 0,452 | 0,625 | 0,789 | 0,911 |
| $u=u_{correcta}$ | 0,726 | 0,548 | 0,375 | 0,202 | 0,089 |
o simplemente repartir de forma equitativa la probabilidad entre las respuesta incorrectas:
| $\theta=\theta_E$ | $\theta=\theta_D$ | $\theta=\theta_C$ | $\theta=\theta_B$ | $\theta=\theta_A$ | |
|---|---|---|---|---|---|
| $u=u_{correcta}$ | 0,274 | 0,452 | 0,625 | 0,789 | 0,911 |
| $u=u_{incorrecta_1}$ | 0,242 | 0,183 | 0,125 | 0,067 | 0,030 |
| $u=u_{incorrecta_2}$ | 0,242 | 0,183 | 0,125 | 0,067 | 0,030 |
| $u=u_{en blanco}$ | 0,242 | 0,183 | 0,125 | 0,067 | 0,030 |
lo que en la práctica produce los mismos resultados dado que la forma de las curvas es homotética y finalmente se procede a su normalización.
Modelos paramétricos
La teoría de respuesta al ítem clásica se basa en establecer modelos contínuos en donde una variable $\theta$ toma valores en el intervalo real $[-\infty,+\infty]$. El modelo mas simple es el modelo dicotómico en el que cada para cada una de las preguntas se consideran solamente dos casos: respuesta correcta o incorrecta (considerando también la respuesta en blanco como respuesta incorrecta). Los modelos mas comunes se basan en funciones características basadas en la función logística con uno, dos o tres parámetros:
Modelo de Rasch (1PL)
El caso mas simple se basa en suponer que la probabilidad condicionada o curva característica de la respuesta correcta a una pregunta i-esima viene dada por la función logística: $$p_i(\theta) = \frac{1}{1+e^{-Da(\theta-b_i)}}$$
en donde $p_i(\theta)$ es la probabilidad de que un alumno con nivel de conocimiento $\theta$ conteste correctamente a la pregunta i-esima. $b_i$ es un parámetro denominado “dificultad” variable para cada ítem; $a$ es un parámetro denominado “discriminación” que es igual para todos los ítems y $D$ es una constante cuyo valor es 1,702 que hace que la función logística tenga un mayor parecido con la función de distribución (probabilidad acumulada) de la normal $N(0,1)$.
El parámetro $b_i$ corresponde al nivel de conocimiento para el cual es igualmente probable que la respuesta sea correcta o incorrecta. El parámetro $a$ es proporcional a la máxima pendiente de la curva, que se produce precisamente para el valor $\theta=b_i$.
Modelo 2PL
En este caso se asume que las curvas características vienen dadas por dos parámetros para cada pregunta, es decir, que el parámetro $a_i$ puede ser diferente para cada pregunta: $$p_i(\theta) = \frac{1}{1+e^{-Da_i(\theta-b_i)}}$$
Modelo 3PL
En este caso se añade a la curva característica de cada pregunta un tercer parámetro $c_i$ denominado “adivinanza”, que representa la probabilidad de que un alumno sin ningún conocimiento del tema responda correctamente a la pregunta por azar: $$p_i(\theta) = c_i + (1-c_i)\frac{1}{1+e^{-Da_i(\theta-b_i)}}$$
Modelo 4PL
Es un modelo no estándar que introduce Siette, añadiendo un cuarto parámetro $d_i$ llamado “distracción”, que representa la probabilidad de que un alumno, aunque tenga un conocimiento completo del tema, responda incorrectamente debido a cualquier factor fortuito o imprevisto (por ejemplo se salte una pregunta sin querer, o se confunda al seleccionar la respuesta en el interfaz de respuesta). En este caso la curva característica sería $$p_i(\theta) = c_i + (1-c_i-d_i)\frac{1}{1+e^{-Da_i(\theta-b_i)}}$$ El mínimo de esta función es $c_i$ y máximo $1-d_i$
Interpretación de los parámetros
En los siguientes ejemplos se muestra como varían las curvas características en función de los valore de los parámetros. En las imágenes la escala horizontal se ha modifcado utilizando el intervalo $[0,10]$ para que resulte mas intuitivo.
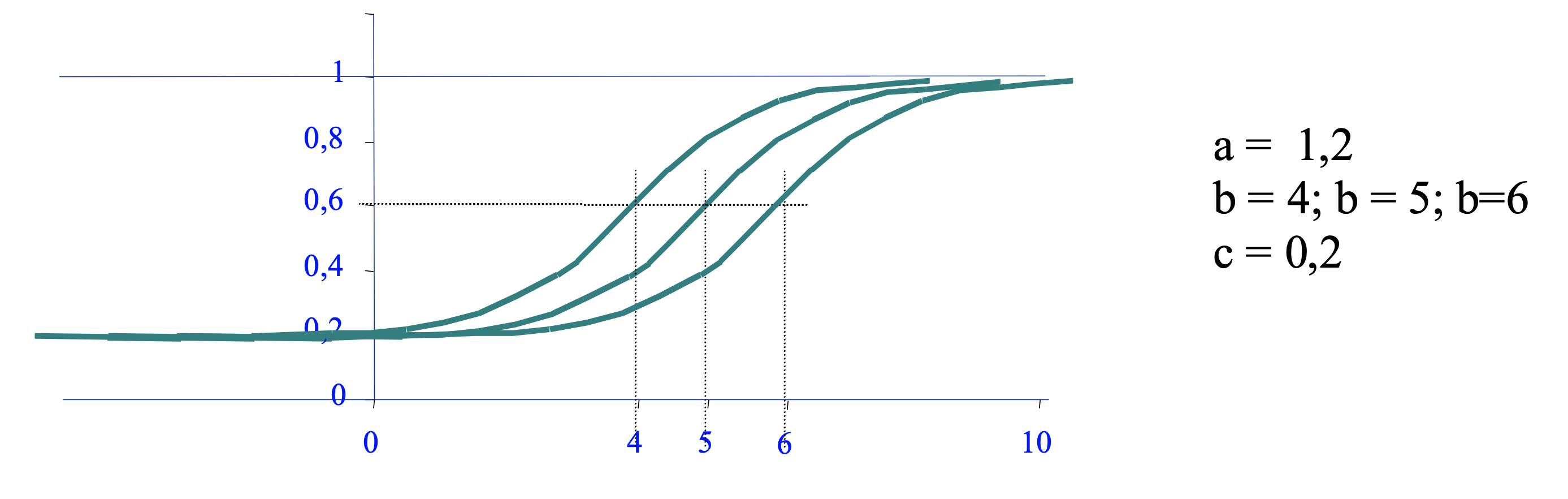
Dificultad
El parámetro $b_i$ se corresponde con la noción intuitiva de “dificultad de una pregunta”. Una preguntas mas difícil tendrá un parámetro $b_i$ mas alto. Al aumentar este parámetro la curva característica se desplaza hacia la derecha, y al disminuir, hacia la izquierda
En el modelo de 1PL, el valor de $\theta = b_i$ coincide con el punto de inflexión de la curva en el que el valor de la probabilidad es exactamente $p(\theta=b_i)=0,5$. En el caso del modelo de 3PL, el valor en $\theta = b_i$ coincide con el punto de inflexión, pero el valor de la probabilidad es $p(\theta=b_i)=c_i+(1-c_i)/2$
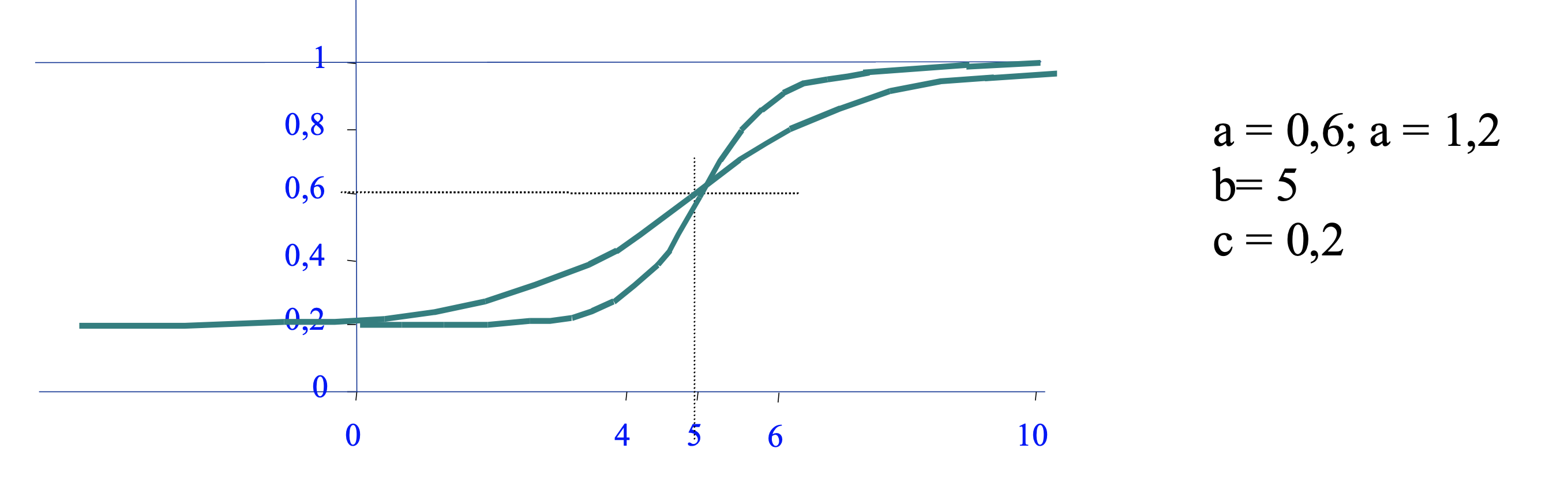
Discriminación
El parámetro $a_i$ modifica la pendiente de la curva. Cuanto mayor sea $a_i$ mayor será la pendiente de la curva en todos los puntos, y especialmente en el punto de inflexión para el que se produce la pendiente máxima.
Este parámetro se llama “factor de discriminación” porque al ser mayor indica que la respuesta a esta pregunta es capaz de discernir con mayor facilidad entre un alumno con conocimiento mayor o menor que el nivel de dificultad $b_i$. Cuando el parámetro $a_i$ es pequeño, la curva característica se aplana, tiene una pendiente pequeña y las probabilidades de respuesta correcta no dependen tanto del nivel de conocimientos del alumno, es decir, la pregunta no discrimina bien.
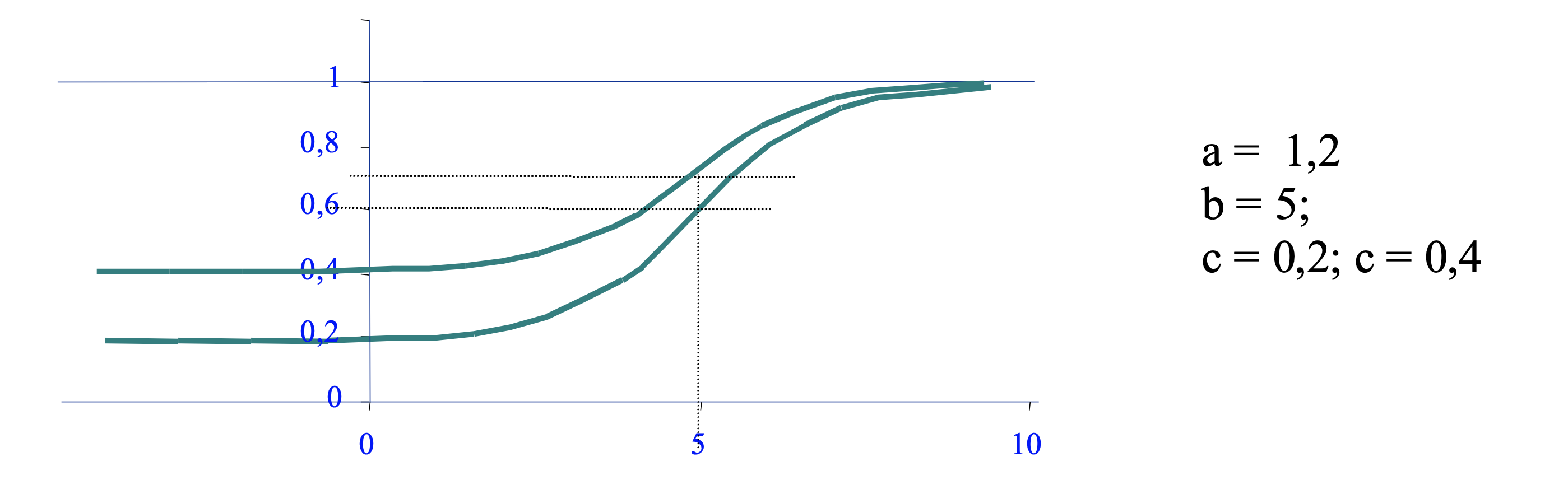
Adivinanza
El parámetro $c_i$ modifica el valor de la probabilidad en el extremo izquierdo del intervalo, es decir, la probabilidad de contestar correctamente la pregunta sin tener conocimiento alguno de la materia, or lo que se denomina “factor de adivinanza”.
Al aumentar el valor del factor de adivinanza, disminuye automáticamente la pendiente de la curva. En principio, podría pensarse que el factor de adivinanza tiene que ver con el número de opciones de respuesta. Por ejemplo, una pregunta con tres opciones de respuesta, en la que el alumno sabe que solo una de ellas es correcta tendría al menos un valor $c_i=0,333$. Una pregunta de respuesta abierta en la que hay que escribir el resultado tendría un coeficiente $c_i=0$. Estos valores que pueden establecerse simplemente observando las posibilidades de respuesta de la pregunta son valores mínimos. En la práctica las probabilidades de acierto al azar pueden ser algo mayores.
En cualquier caso tanto éste como los demás parámetros de las curvas deben obtenerse mediante un proceso de calibración a la vista de los resultados de una muestra.
Discretización de los modelos paramétricos
Cualquier modelo paramétrico puede convertirse en un modelo no-paramétrico simplemente tomando los valores de probabilidad en determinados puntos. Este procedimiento simplifica el cálculo de probabilidades y facilita la estimación de las curvas características en el caso de que no se disponga de suficientes datos para calibrar un modelo politómico no-paramétrico.
Por ejemplo, para una asignatura con 10 niveles de conocimiento en la que mediante técnicas de calibración estandar se han obtenido para una pregunta los parámetros a=1.2; b=1.4; c=0.1; la discretización da como resultado la siguiente tabla de probabilidad condicionada:
| $\theta=\theta_0$ | $\theta=\theta_1$ | $\theta=\theta_2$ | $\theta=\theta_3$ | $\theta=\theta_4$ | $\theta=\theta_5$ | $\theta=\theta_6$ | $\theta=\theta_7$ | $\theta=\theta_8$ | $\theta=\theta_9$ | |
|---|---|---|---|---|---|---|---|---|---|---|
| $u=u_{correcta}$ | 0,100 | 0,101 | 0,102 | 0,108 | 0,127 | 0,186 | 0,338 | 0,596 | 0,826 | 0,941 |
Análogamente, dada una tabla con un conjunto de valores correspondientes a la probabilidad condicionada para $K$ niveles de conocimiento, se puede obtener mediante la técnica de mínimos cuadrados los valores de los parámetros de la curva mas cercana de entre las curvas de esta familia de curvas.
Modelo contínuo
Actualmente la potencia de cálculo de los ordenadores permite aplicar sin problemas el modelo contínuo, que en la práctica no es mas que el mismo modelo discreto en el que el número de intervalos es suficientemente alto. Muchas de las ecuaciones de los modelos de TRI no tiene una solución algebraica por lo que es común recurrir a modelos de cálculo numérico en intervalos infinitesimales.
En la práctica se usan 100 intervalos ya que la diferencia entre los resultados son inapreciables utilizando una discretización mas fina y las aproximaciones son suficientemente buenas en comparación con el ajuste del modelo a la realidad 1).