Tabla de Contenidos
Concepto de evaluación y modelos del conocimiento
NOTA: Este capítulo esta escrito informalmente, a modo de divulgación científica. Existe una amplia bibliografía a la que remitimos al lector interesado en profundizar sobre este tema.
La ciencia se basa en crear modelos de la realidad. En el caso de la evaluación el objeto de estudio es el conocimiento que un alumno tiene de una determinada materia. Evidentemente, la complejidad del cerebro humano, sus conexiones neuronales, la memoria, el razonamiento y todo aquello que constituye lo que llamamos “conocimiento” es demasiado complejo y en gran parte desconocido. Por consiguiente, se recurre a modelos aproximados para “medir” de alguna forma este conocimiento.
Para que exista ciencia deben existir modelos científicos que expliquen sucesos o verdades y que sean totalmente aplicables a la realidad Karl Popper
Modelos clásicos
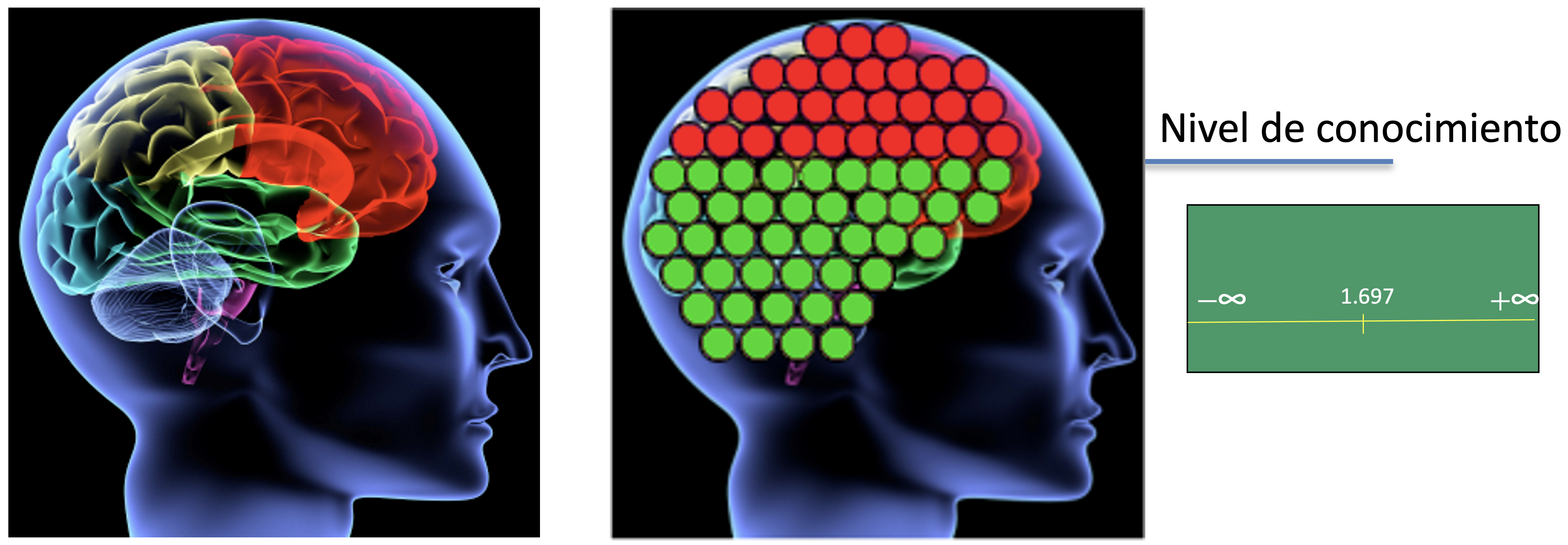
Los modelos mas simples y mas usados en la práctica se reducen a un simple valor numérico, al que se denomina “nivel de conocimiento”, sobre una materia en concreto. Así por ejemplo, los profesores acostumbran a poner notas a los alumnos que indican si saben mas o menos sobre una materia. Esta nota es una especie de aglutinante de los conceptos que el alumno tiene sobre la materia.
En esencia este modelo se basa en suponer que el conocimiento de una materia esta formado por una infinidad de pequeños conceptos indivisibles (entendiendo como tales los hechos, relaciones, análisis, inferencias, criticas, etc) sobre la materia. En la imagen anterior se representan como bolitas, en verde y en rojo (conocidas y desconocidas por el alumno). El nivel de conocimiemntos en este caso podría interpretarse como el número de “bolitas” que hay de cada color. El procedimiento para inferir el número total de “bolitas verdes” dentro del cerebro consiste en ir sacando “bolitas” mediante preguntas concretas al azar (generalmente de opción múltiple) que se acertarán solo si el concepto subyacente se conoce. En realidad el problema es aun mayor ya que se puede dar el caso en el que un concepto no se conozca pero se responda correctamente por azar, o viceversa. Es como si algunas “bolitas”, al sacarlas pudieran cambiar de color.
Las principales teorías sobre la evaluación surgidas en el siglo XX, la teoría clásica de los test y la teoría de respuesta al ítem, se basan en este modelo y obtienen como representación del conocimiento del alumno un número real relativo a una escala, que puede ser de 0 a 10, o de $-\infty$ a $+\infty$.
En muchos casos este modelo es claramente demasiado simple. Dos alumnos con la misma nota puede que no tengan el mismo conocimiento sobre una materia, puede que uno de ellos sepa unos conceptos en concreto y el otro no sepa esos conceptos, y tambien al contrario, aunque probablemente habrá un nucleo común que con mucha probabilidad ambos comparten. Imaginemos por ejemplo dos alumnos con una nota de 9 sobre 10 en la materia “Física”. Puede que uno de ellos haya alcanzado esta nota con algún fallo en los conceptos de “Mecánica”, pero haya alcanzado el máximo en “Electricidad”, mientras que otro alumno con la misma nota haya alcanzado el máximo en la primera, pero no en la segunda
Modelos bayesianos
Evidentemente pueden desarrollarse modelos mas complejos, que tengan en cuenta que los conceptos que intervienen en el conocimiento de una materia no están asilados y que establezcan relaciones entre los conceptos, o el orden en que se aprenden. Estos modelos suelen ser diseñados específicamente para una materia y no directamente utilizables como modelos genéricos, es decir aplicables directamente a cualquier materia, salvo que se realice previamente un proceso de definición del modelo.
En este sentido, Siette incorpora algunas características que pueden servir para crear modelos complejos que proporcionen una descripción mas detallada del conocimiento del alumno, mas allá de un simple valor numérico. Habitualmente estos modelos cuantifican las relaciones entre conceptos mediante probabilidades condicionales o establecen relaciones de causalidad formando lo que se conoce como redes bayesianas.
Por otra parte, Siette incorpora tambien mejoras en cuanto a la obtención de evidencias en este proceso, incorporando diversos tipos de preguntas que permiten, siguiendo con el simil anterior, sacar muchas “bolitas” a la vez y atenuar la posibilidad de error.
Modelo jerárquico
El modelo jerárquico consiste simplemente en establecer una jerarquía entre el conjunto de conceptos que componen una materia. La jerarquía es simplemente una relación de tipo “es-parte-de”, por ejemplo podriamos decir que el concepto “Suma” es parte del concepto “Aritmetica” y éste a su vez del concepto “Matemáticas”, o que los conceptos “Mecánica” y “Electricidad” son partes del concepto “Física”, etc. En la terminología de Siette estos conceptos equivalen a Temas y Subtemas.
En Siette el profesor puede crear un curriculum o jerarquía de temas y subtemas y asociar las preguntas cada uno de estos temas o subtemas. Al realizar una evaluación Siette asume que para evaluar un tema puede utilizar todas las preguntas asociadas directamente a ese tema o a alguno de sus subtemas. Una vez completada la evaluación, Siette puede proporcionar información acerca del conocimiento del alumno en el tema objeto del test, pero tambien en cada uno de los subtemas que lo componen. Para ello simplemente obtiene la calificación usando las preguntas asociadas a cada subtema.
Evidentemente, si el test se componen de 50 preguntas y tiene 5 subtemas, cada uno de ellos puede tener una media de 10 preguntas, y si a su vez cada subtema tiene otros 5 subtemas, de cada sub-subtema se habrán realizado solamente 2 preguntas. Evidentemente la precisión de la medida sería muy baja en este caso. Esta precisión corresponde claramente con el posible error de la medida, y puede medirse mediante la desviación tipica o el error estandar, o incluso mejor mediante el concepto de fiabilidad.
Modelo de prerequisitos
Siette incorpora la posibilidad de que el profesor establezca para una materia un modelo basado en prerequisitos. Un prerequisito se entienede en Siette como la relacion “es-necesario-para-saber”, por ejemplo, “Sumar” es necesario para saber “Multiplicar”. Hay mucha complejidad inherente al concepto de prerequisito, y es actualmente un campo de investigación abierto.
Dotar de una semántica clara al concepto de prerequisito no es fácil, y diversos autores utilizan con el mismo nombre diversas implementaciones de este concepto. Podría hablarse de requisitos fuertes y débiles, por ejemplo la semántica de un prerequisito fuerte podria ser “Es imposible que un alumno sepa lo mas mínimo del concepto B si no sabe del concepto A”. Evidentemente esto solo es aplicable si los conceptos A y B son atómicos, es decir indivisibles, o se saben o no se saben. Sin embargo en la práctica los requisitos siempre son débiles en cierta medida. Por ejemplo un alumno puede saber algunas tablas de multiplicar y resolver algunos problemas de multiplicaciones sin haber alcanzado la capacidad de sumar con acarreo. Como puede verse, el problema se plantea porque tanto el coepto “Suma” como el concepto “Multiplicar” son en realidad conceptos que a su vez pueden dividirse en otros mas simples y así sucesivamente.
Actualmente Siette permite al profesor declarar los prerequisitos entre temas y subtemas (conceptos), pero no se ha establecido aún una semántica clara y una aplicación o inferencia a partir de esta relación. Definir estas relaciones permitirá realizar inferencias mas allá de la medida directa del conocimiento de un tema o concepto. Por ejemplo, estableciendo que el nivel de conocimienmto en el tema “Multiplicar” es muy alto, se podría inferir que el nivel de conocimiemto en “Suma” tambien lo es, o por el contrario, si el nivel en “Suma” es muy bajo, podriamos presumir que el nivel en “Multiplicación” no alcanzará el máximo. Cuantificar este tipo de relaciones es actualmente objeto de investigacion.
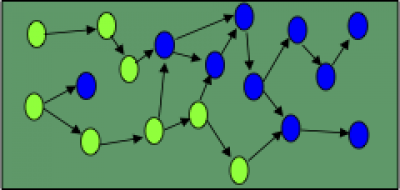
Por el momento, la relación de prerequisito solo se usa para constrir un grafo mediante el sistema de representación de modelos de conocimiento Ingrid para mostrar tanto al alumno como al profesor una información visual mas atractiva y compacta.
Modelo de errores conceptuales
Los modelos anteriores se basan en elicitar los conceptos que componen una materia y las relaciones entre ellos. Sin embargo, existen otro tipo de modelos que consisten en identificar errores comunes en el aprendizaje de una materia a los que llamaremos errores conceptuales. Por ejemplo, un error típico de los alumnos cuando estudian la suma es olvidar el acarreo, lo que conlleva que que la respuesta a la pregunta es “¿Cuanto es 27+38?” sea “55” en vez de “65”, etc.
Evidentemente cada materia y en concreto cada tema y subtema tendrán sus propios posibles errores conceptuales, que estarán asociados a determinadas respuestas incorrectas a las preguntas de ese tema o subtema. Para usar este modelo, al crear la pregunta, el profesor debera asociar a cada una de las opciones de respuesta un posible error conceptual. La elección sistematica de las opciones de respuesta asociadas a ese error en distintas preguntas será la evidencia que permita diagnosticar este error conceptual para un determinado alumno.
El disgnóstico de rrores conceptuales es ortogonal al diagnóstico del nivel de conocimiento, es decir, es una información adicional que puede hacerse solo si el profesor ha añadido la correspondiente asociación entre respuesta y error, pero que no afecta para nada a la medida de la evaluación del tema.
Aunque esta funcionalidad lleva tiempo implementada en Siette, actualmente son muy pocos los casos en los que los profesores han definido errores conceptuales.