Patrón de expresiones matemáticas
Este patrón esta diseñado para reconocer como respuesta una función matemática de una o dos variables. El patrón describe una función y las respuestas deben describir la misma función aunque no necesariamente con idéntica expresión matemática. Por ejemplo la función $x^2-1$ puede escribirse de múltiples formas, por ejemplo $-1+x*x$ o bien $(x-1)(x+1)$, y muchas más, todas ellas equivalentes a la forma que se da como nominal.
Uso del patrón
Para escribir un patrón de expresiones matemáticas, el profesor tiene que proporcionar una forma cualquiera de la función, escrita en una versión reducida del lenguaje LaTeX. Opcionalmente la fórmula puede empezar y terminar con uno o dos símbolos $. Existen muchos editores que permiten crear este tipo de fórmulas. En muchos casos, el profesor que utiliza fórmulas matemáticas puede escribir el patrón sin necesidad de usar ningún editor. Igualmente el profesor debe introducir un ejemplo válido, que por lo general coincide con el patrón.
Ejemplo 1
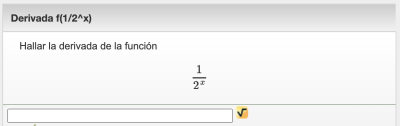
| Enunciado | Hallar la derivada de la función \$\$\frac{1}{2^x}\$\$ |
|---|---|
| Patrón. | -ln(2)/2^x |
| Respuestas reconocidas | \$-ln(2)/2^x\$ |
| \$\frac{-\ln(2)}{2^x}\$ | |
| -\ln(2)2^{-x} | |
| \$e^{-x\ln(2)}\left(-\ln(2)\right)\$ |
En asignaturas que utilicen este tipo de fórmulas es normal que esté activada la opción de utilizar fórmulas en MathJax, por lo que las fórmulas que el profesor utilice en el enunciado y en el ejemplo normalmente serán transformadas por MathJax en una representación visual, ocultando el código LaTeX. La siguiente imagen muestra la presentación de la pregunta anterior:
Cuando se usa el patrón de expresiones matemáticas, el interfaz del alumno incluye MathType, un pequeño editor de formulas, de manera que el alumno no tenga que recordar la escritura en LaTeX. No obstante, la respuesta también puede escribirse directamente sin utilizar ningún editor.
La comprobación de equivalencia entre la respuesta del alumno y el patrón propuesto por el profesor no utiliza ninguna transformación algebraica, sino una mera comprobación numérica en un conjunto de puntos, algunos generados de forma aleatoria y otros correspondientes a puntos singulares, como 0,1, $\pi$; $e$, $\pi/2$, etc. (Por cada función se prueban alrededor de 1000 puntos aleatorios y 50 puntos singulares). Si el resultado de la función patrón es el mismo en todos los puntos que la evaluación de la función escrita por el alumno (salvo un error $\epsilon$), la respuesta se considera que encaja con el patrón. Este mecanismo no es infalible pero funciona bien para la mayoría de las aplicaciones.
Ejemplo 2
| Enunciado | Escribir la expresión correspondiente al lugar geométrico de los puntos de un circulo de radio 2 y centro en el punto (1,0) |
|---|---|
| Patrón. | (x-1)^2+y^2 = 4 |
| Respuestas reconocidas | \$(x-1)^2+y^2 - 4 = 0\$ |
| (x-1)^2 = 4 - y^2 | |
| x^2-2x+y^2 = 3 | |
| Respuestas no reconocidas | y=\sqrt{3+2x-x^2} |
El patrón puede utilizar funciones de dos variables y acepta el operador =, de manera que pueden emplearse funciones implicitas o explicitas. Sin embargo, hay algunas excepciones que deben tenerse en cuenta, dado el funcionamiento del patron. En el ejemplo anterior, la expresión $y=\sqrt{3+2x-x^2}$ no se considera correcta, ya que al evaluar por ejemplo para el puntos (-2,1), se obtiene -2 en la parte izquierda de la igualdad y $\sqrt{4}$ en la parte derecha. El computo de esta función en el ordenador devuelve solamente el valor positivo 2, (en vez de $\pm2$), por lo que $-2\neq2$ y la expresión falla.
Por otra parte, cuando el resultado de la operacion esinfinito, no se tiene en cuenta el signo en la comparación, de manera que los infinitos positivo y negativo se consideran iguales, por ejemplo: -1/0 == 1/0
Al igual que en otras preguntas que usen patrones, el sistema soportan múltiples patrones, unos correctos y otros incorrectos, que pueden servir para diagnosticar errores comunes o errores conceptuales. Nunca se distingue entre mayúsculas y minúsculas y los espacios en blanco no son significativos a menos que afecten a la fórmula en LaTeX.
Aspectos léxicos de las expresiones
La siguiente lista incluye los símbolos e instrucciones de LaTeX soportados por el patrón de matemáticas:
= + - * / ^ _ ( ) [ ] { } ; & \\ |
\ast \times \div \frac \sqrt \abs \pi \infty
\sin \cos \tan \sec \csc \cot
\ln \log_2 \log_10 \log
\left) \left{ \left[ \left| \right) \right} \right] \right|
\begin{\vmatrix} \begin{\bmatrix} \begin{\pmatrix}
\end{\vmatrix} \end{\bmatrix} \end{\pmatrix}
\textstyle \mathrm \circ \color
\Theta \Omega
Además el patrón Siette soporta algunas extensiones léxicas para aceptar como correctas expresiones escritas por el alumno directamente y que se parecen, aunque no son aceptadas por LaTeX, y que son utilizadas usualmente como notación de la correspondiente función:
sqrt raiz abs seno sen sin coseno cos tangente tan tg secante sec cosecante csc cotangente ctg cot ln log2 log_2 log10 log_10 log
El patrón de matemáticas también asigna valores predeterminados a los siguientes caracteres:
| i | $\sqrt{-1}$ |
|---|---|
| $\pi$ | 3.14159265359 |
| e | 2.71828182846 |
| x | primera variable por defecto |
| y | segunda variable por defecto |
Variables
La respuesta al patrón es una función de una o dos variables. Los nombres de las variables por defecto son x e y. Si no se especifica otra cosa, el patrón espera que el alumno utilice estos mismos nombres como respuesta. Sin embargo, en el caso de que la respuesta del alumno no incluya ninguna de estas variables, cualquier otro nombre de variable de una sola letra (salvo la e que representa a la constante de Euler) se tomará como primera y segunda variable, siguiendo el orden léxico. Las únicas excepciones son las propias variables x e y que siempre se representan a sí mismas como primera y segunda variables respectivamente.
Ejemplo 3
| Patrón. | y + x^2</b> |
|---|---|
| Respuestas reconocidas | y + x^2 |
| x^2 + y | |
| r^2 + s | |
| x^2 + s | |
| z^2 + y | |
| Respuestas no reconocidas | r + s^2</nowiki> |
| s^2 + r |
En el ejemplo 2, si el alumno responde: r^2 + s; la r se considerara como primera variable (representa a la x) y la s la segunda (representa a la y), encajando con un patrón como y + x^2. Sin embargo, si la respuesta fuera x^2 + s, se seguiría tomando que la s como segunda variable, a pesar de que el orden léxico entre primera y segunda variable no se cumpla. También en el caso de que la respuesta sea z^2 + y se interpreta que z representa a la primera variable y la y a la segunda.
Sin duda, aunque el patrón lo permita, no conviene abusar de esta flexibilidad, y siempre que sea posible el enunciado debe indicar claramente qué variables deberá utilizar el alumno.
Matrices
El patrón de matemáticas permite también el uso de matrices de funciones. Cuando se comprueba la igualdad entre dos matrices se comparan primero las dimensiones de cada matriz, si las dimensiones coinciden se comprueba uno a uno los pares de elementos de las matrices, que a su vez pueden ser funciones. Si todos encajan, las matrices son equivalentes.
Ejemplo 4
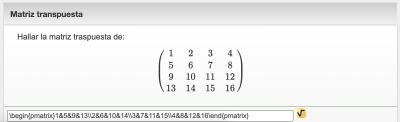
| Enunciado | Hallar la matriz traspuesta de: \$\$ \begin {pmatrix}1&2&3&4\\5&6&7&8\\9&10&11&12\\13&14&15&16\end{pmatrix}\$\$ |
|---|---|
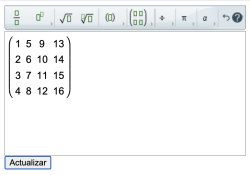
| Patrón. | \$\begin {pmatrix}1&5&9&13\\2&6&10&14\\3&7&11&15\\4&8&12&16\end {pmatrix}\$ |
| Respuestas reconocidas | \$\begin {pmatrix}1&5&9&13\\2&6&10&14\\3&7&11&15\\4&8&12&16\end{pmatrix}\$ |
En el ejemplo 4 se muestra un uso sencillo del patrón para matrices. En estos casos, el uso del editor de ecuaciones se hace practicamente imprescindible.
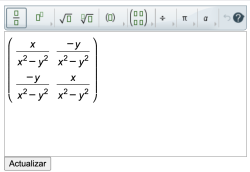
Ejemplo 5
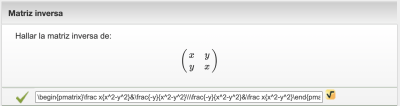
| Enunciado | Hallar la matriz inversa de: \$\$\begin {pmatrix}x&y\\y&x\end{pmatrix}\$\$ |
|---|---|
| Patrón. | \$\begin {pmatrix}\frac x{x^2-y^2}&\frac{-y}{x^2-y^2}\\\frac{-y}{x^2-y^2}&\frac x{x^2-y^2}\end{pmatrix}\$ |
| Respuestas reconocidas | \$\begin {pmatrix}\frac{-x}{y^2-x^2}&\frac y{y^2-x^2}\\\frac y{y^2-x^2}&\frac{-x}{y^2-x^2}\end{pmatrix}\$ |
| Respuestas no reconocidas | \$\frac{\begin {pmatrix}x&-y\\-y&x\end{pmatrix}}{x^2-y^2}\$ |
El ejemplo 5 muestra un caso en el que los elementos de la matriz son a su vez funciones. Por el momento el patrón de matemáticas no soporta operaciones entre matrices ni operaciones entre escalares y matrices.