Desde el punto de vista de la TRI, lo que define una pregunta es su curva característica, que en su caso viene dado por los parámetros de factor de discriminación, factor de dificultad, factor de adivinanza y el factor de distracción, en el modelo de cuatro parámetros: ¹⁾

$$p_i(\theta) = c_i + (1-c_i-d_i)\frac{1}{1+e^{-Da_i(\theta-b_i)}}$$

La curva característica ofrece mucha información sobre el comportamiento del ítem. La dificultad corresponde al punto de inflexión de la curva. Teóricamente, y descontando el factor de adivinanza y distracción, es el valor del nivel de conocimiento tal que la mitad de los alumnos contestan correctamente a esta pregunta y la otra mitad la fallan. Aunque la definición es diferente, está relacionado con el índice de dificultad de la TCT.

El factor de discriminación es una medida similar al índice de discriminación, pero ofrece una mayor información, ya que determina la pendiente de la curva característica. Un factor de discriminación bajo, indicaría que independientemente del nivel de conocimiento, los alumnos tienen una probabilidad similar de contestar correctamente al ítem.

El factor de adivinanza, como su nombre indica, señala la probabilidad de que un alumno sin conocimiento alguno de la materia conteste correctamente a la pregunta. Nótese, que en los ítems de múltiple opción y respuesta única, este valor es al menos superior al inverso del número de opciones, aunque podría incluso ser mayor, si por algún defecto alguna de las opciones puede ser descartada. Por otra parte, aunque teóricamente es nulo en las preguntas de respuesta libre, en la práctica no lo es, ya que siempre puede existir la posibilidad de que se infiera la respuesta por el contexto de la pregunta, alguna pista del enunciado o el mero azar. Por otra parte, un mayor valor de este factor implica que la pendiente de la curva sea menor, para un mismo valor del factor de discriminación.

El factor de distracción no es habitual en los modelos paramétricos de la TRI. Se ha incorporado en Siette como modificación de la curva para adaptarla a casos prácticos en los que se ha detectado que esta circunstancia ocurre. A veces, aunque un alumno tenga un conocimiento completo de un tema, la respuesta a alguna pregunta puede ser incorrecta, simplemente debido al cansancio o a una distracción momentánea. Este fallo espurio no debe interpretarse como falta de conocimiento, sino simplemente como una distracción. Aún así, los valores de este factor deben ser siempre bajos.

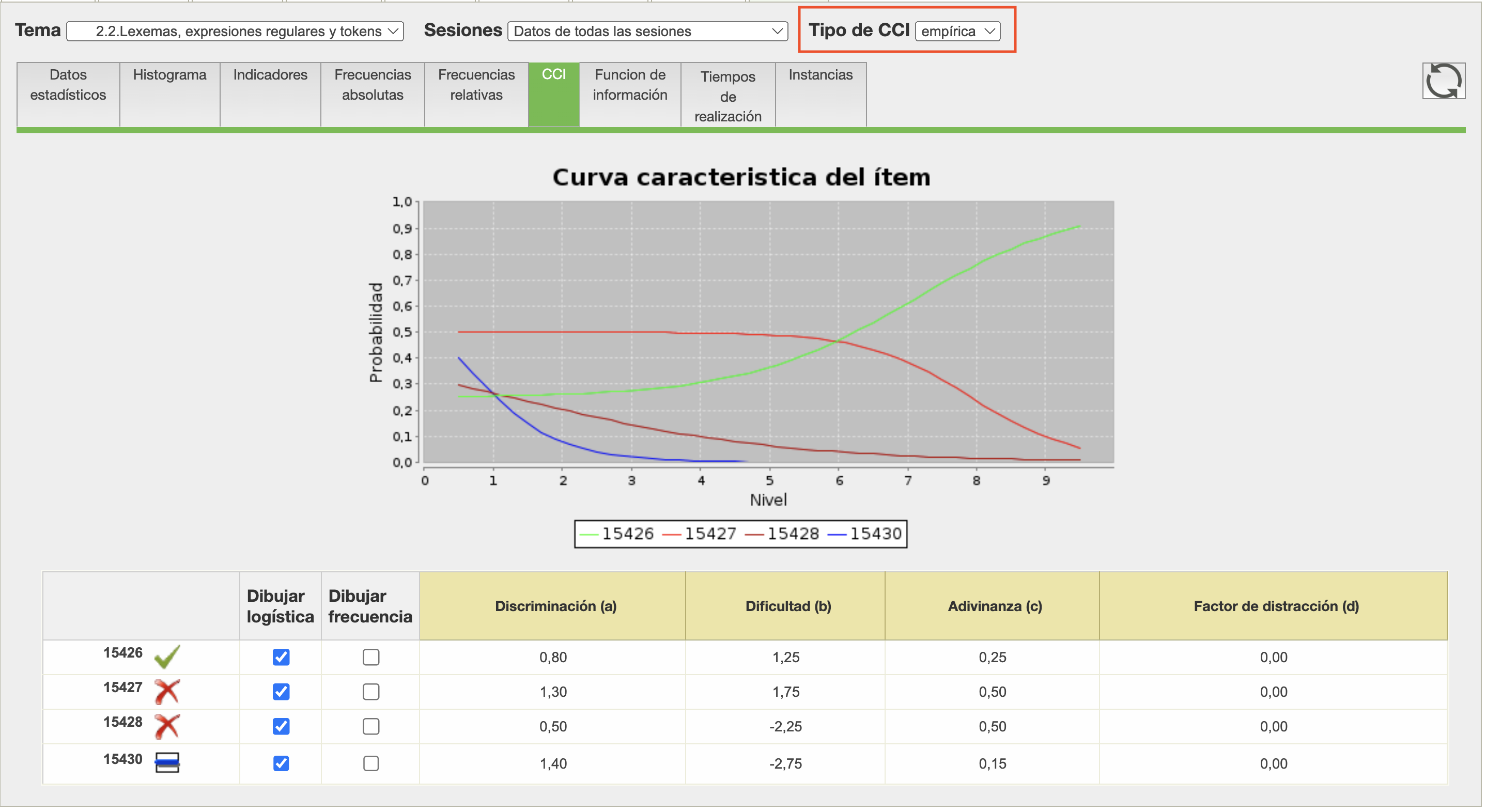
Para visualizar la curva característica de un ítem en el editor, hay que acceder a la subpestaña CCI de la pestaña Analizador en la sección Preguntas. En esta pestaña se muestra no solo la curva característica de la opción correcta, sino tambien las curvas características de las opciones de respuesta o patrones incorrectos.

Una forma de aproximar las curvas características es mediante la interpolación directa de los datos obtenidos en las sesiones de test en los que ha intervenido la pregunta, tomando como valor del nivel de conocimiento del alumno, el valor final de la evaluación, aunque éste haya sido obtenido simplemente or el porcentaje de aciertos o la puntuación. Es decir, suponer que la calificación a priori es correcta e interpolar curvas paramétricas para cada una de las opciones de respuesta. A estas curvas se les llama curvas características empíricas, y constituyen el primer paso del proceso de calibración. Es importante comprobar que hay suficientes datos para obtener buenas interpolaciones, especialmente en las opciones que se seleccionan con menor frecuencia.

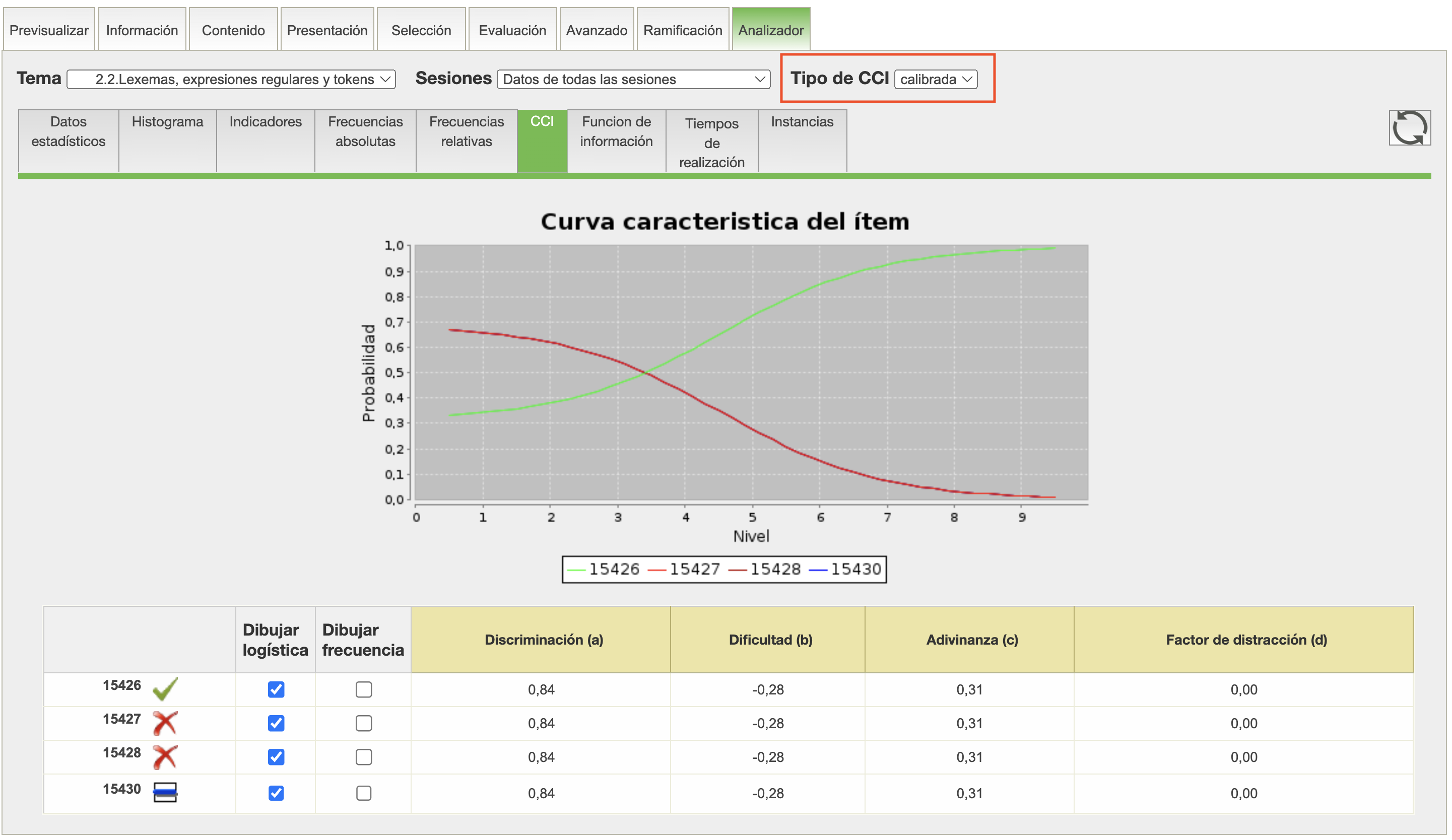
Las curvas características de los ítems se obtienen mediante un proceso de calibración. Supuestamente, los valores de los parámetros son invariantes, y no dependen del nivel de conocimiento de los alumnos cuyos datos se han usado para calibración. Desde un punto de vista práctico esta afirmación no siempre es cierta, ya que los modelos no son sino aproximaciones imperfectos de una realidad compleja.

En muchas ocasiones, por falta de datos suficientes no es posible alcanzar una calibración politómica. La calibración en estos casos es dicotómica, ya que solo calcula la curva característica de la opción de respuesta correcta, agrupando todas las demás opciones en la curva complementaria de la opción correcta.

Si se han calibrado bien las curvas, y se han aplicado posteriormente en la obtención de los valores del nivel de conocimiento usando el mecanismo de evaluación de la TRI, las curvas empíricas y calibradas deben ser similares. Puede haber discrepancias si no se ha empleado el método de evaluación TRI, o por otros motivos, como falta de adecuación al modelo a la realidad, escasez de datos en la calibración, etc. En cualquier caso es conveniente que estas discrepancias se mantengan dentro de límites razonables.

Por otra parte, Siette utiliza un modelo jerárquico de temas y subtemas, y asume que cada pregunta puede tener curvas características diferentes dependiendo del tema o subtema que esté evaluando. Por ejemplo, una pregunta sobre la velocidad de un vehiculo puede tener una curva característica diferente para el tema Física o para los subtema Mecánica y mas concretamente Movimiento uniforme. Intuitivamente se comprende que la dificultad de esta pregunta no es la misma si lo que se quiere es obtener el nivel de conocimiento de un alumno en el tema Física o en temas mas específicos. Por esta razón Siette utiliza curvas características diferentes para cada uno de os temas y subtemas, que se obtienen empíricamente o mediante calibración a partir de las calificaciones obtenidas en cada uno de los temas y subtemas.

Cuando se quieren comparar las curvas características de varios ítems, debe seleccionarse la opción TRI en la pestaña Indicadores de las secciones de Test o Temas, según el conjunto de ítems que se quiera analizar. En este caso se muestran solamente los valores de los parametros de la curva corre cta.

La función de información del ítem puede calcularse mediante la formula:

$$I(\theta) = D^2a^2 \left( \frac{(P(\theta)-c+d)^2}{(1-c+d)^2} \frac{(1-P(\theta))}{P(\theta)} \right)$$

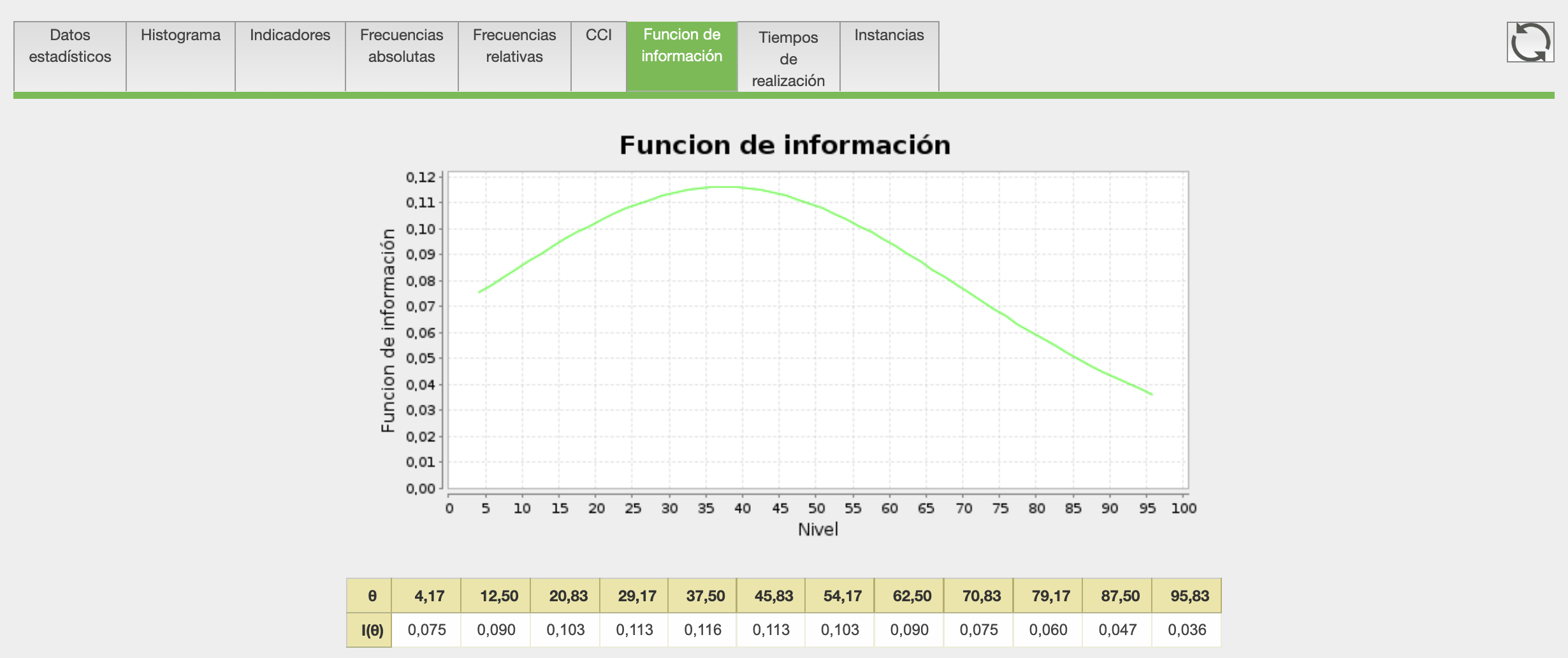
Esta curva deriva de la curva característica del ítem y tiene su máximo cerca del valor de la dificultad, del ítem. Los valores altos de esta curva indican los niveles de conocimiento para los cuales este ítem da una mayor información. Para valores bajos, el ítem no es apropiado ya que con alta probabilidad los alumnos acertarán o fallarán previsiblemente. Esta curva resumen los razonamientos efectuados anteriormente sobre la curva característica teniendo en cuenta conjuntamente la influencia de los distintos factores.

Para visualizar la función de información de un ítem en el editor, hay que acceder a la subpestaña Función de información de la pestaña Analizador en la sección Preguntas. La función de información corresponde a la opción de respuesta correcta.