Table of Contents
Evaluación de las preguntas
Entendemos por modelos de evaluación el algoritmo según el cuál se obtiene a partir de las respuestas del alumno una estimación de su nivel de conocimientos, ya sea en una escala numérica o en un conjunto de valores en los que se le clasifica.
Dependiendo del tipo de pregunta y del tipo de evaluación se usan distintos parámetros. El siguiente es un cuadro resumen de los valores por defecto. En las siguientes secciones se explica y justifica cada caso en detalle y se comentan las posibles modificaciones de este comportamiento por defecto.
| Respuesta única | Respuesta múltiple | Respuesta libre | |
|---|---|---|---|
| Porcentual | La respuesta es correcta si se ha seleccionado la opción marcada como Correcta | La respuesta es correcta si se ha seleccionado todas las opciones marcadas como Correcta y ninguna de las marcadas como Incorrecta | La respuesta es correcta si encaja con algún patrón marcado como Correcto |
| Por puntos | Si la respuesta es correcta se asigna 1 punto, si es incorrecta se asigna $-\frac{1}{K-1}$, siendo $K$ el número de opciones de la pregunta | Cada opción de respuesta puntúa con $+\frac{1}{K}$ puntos en caso de que la opción sea Correcta y el alumno la seleccione o bien sea Incorrecta y el alumno no la seleccione,; y con $-\frac{1}{K}$ en caso contrario. | Si la respuesta encaja con algún patrón señalado como Correcto se le asigna 1 punto positivo, en otro caso no se asigna ninguna puntuación |
| TRI | La opción de respuesta correcta tiene una curva característica propia, $p(\theta)$ , las respuestas incorrectas y las respuesta en blanco tienen una curva característica $1-p(\theta)$ 1) | Si la opción seleccionada se corresponde con la corrección propuesta se aplica la curva característica $p(\theta)$; y si no la complementaria $1-p(\theta)$ | Si la respuesta corresponde a un patrón correcto se usa la curva característica $p(\theta)$; y si no la complementaria $1-p(\Theta)$ 2) |
Preguntas de respuesta única
En las preguntas de respuesta única se proponen al alumno varias opciones para que elija una, sabiendo que solo una de las opciones mostrarda es correcta, y las demás son lo que en la jerga de evaluación se llaman distractores. Las posibles acciones del alumno son elegir una de ellas, o no responder a la pregunta y saltar a la siguiente.
Evaluación Porcentual
Para la evaluación porcentual está claro que solo seleccionando la respuesta correcta se considera la pregunta como correcta.
Evaluación Por puntos
En la evaluación por puntos se puede tener en cuenta que el alumno puede seleccionar la opción correcta simplemente por azar. Si suponemos que esto mismo puede ocurrir en otras preguntas similares, y se quiere evitar el efecto del azar de manera que en la evaluación final un alumno que responda al azar obtenga como nota mas probable un 0, hay que descontar puntos en el caso de que la respuesta sea incorrecta, a fin de compensar las respuestas correctas al azar. Por ejemplo, si un test tiene 100 preguntas de tipo verdadero/falso cualquier alumno simplemente por azar acertará un numero considerable de preguntas, cercano a 50 por la ley de los grandes números.
El cálculo es sencillo. Supongamos que todas las preguntas tiene $K$ opciones de respuesta, una sola correcta. La máxima verosimilitud, o caso mas probable es que en un número $N$ suficientemente grande de preguntas el alumno obtenga la respuesta correcta en $K/N$ ocasiones, y la respuesta incorrecta en $(N-K)/N$ ocaciones. Si en cada respuesta correcta ha obtenido 1 punto, y se quiere que la suma final sea 0 para este alumno, habrá que restar $1/(K-1)$ puntos por cada respuesta incorrecta.
Esta corrección lo único que hace es que el valor maximo verosimil de la puntuación sea 0, pero no impide que por efecto del azar sea un poco mayor o incluso menor que 0.
Nótese que esta corrección tambien puede hacerse de otro modo: Considerando el modelo porcentual, es decir, sin descontar ningún punto por las respuestas incorrectas, basta con situar el umbral de conocimiento en un limite superior a 0. En el ejemplo anterior con 100 preguntas de tipo verdadero/falso, este nivel podría situarse en el 50%, es decir, que a los alumnos que obtuviesen esta calificación (o menor) no se les supone conocimiento alguno de la materia.
En el caso de la evaluación por puntos, este mecanismo por defecto asume que las opciones de respuesta son equiprobables, es decir, que un alumno sin conocimiento alguno puede elegir cualquiera de ellas si solo hace una conjetura al azar. Esto no siempre es cierto. Algunas de las opciones de respuesta son claramente inútiles como distractores. Siette permite modificar manualmente los valores asignados tanto a la puntuación de la respuesta correcta como a cada uno de los distractores.
En Siette cada pregunta tiene asociado una puntuacion máxima positiva y una puntuacion máxima negativa. El primer valor corresponde al valor obtenido con la respuesta correcta, y el segúndo al máximo del valor asignado a cualquiera de los distractores.
Asi por ejemplo una pregunta podría asignar como puntuación maxima positiva 2.0 puntos y como puntuación máxima negativa 1.0 punto, distribuyendo la puntuación negativa en sus tres distractores de manera asimetrica, a uno de los distractores le asignaria -1.0 y a otro -0.75 y a otro -0.5
| Puntuación positiva | Puntuación negativa | |
|---|---|---|
| ¿Cómo se llama el tipo de fruto de la fresa? | ||
| Baya | +2.0 | |
| Valla | -1.0 | |
| Vaya | -0.75 | |
| Balla | -0.5 | |
Aunque este tipo de modificaciones en las puntuaciones asignadas por defecto puede hacerse, se desaconseja modificar los valores por defecto, ya que no responden a criterior objetivos. Ademas, tengase en cuenta que las preguntas del banco de preguntas pueden reutilizarse en diversos test, por lo que los valores asignados se aplicarán siempre que se use va pregunta.
Evaluación TRI
En el caso de usar la técnica TRI, Siette esta preparado para utilizar una curva diferente para cada tema a los que pertenece la pregunta y para cada una de las opciones de respuesta, e incluso una curva diferente para el caso de respuesta en blanco. Es decir, si una pregunta pertenece al tema Suma, que es subtema del tema Aritmetica que a su vez es subtema del tema Matemáticas, suponiendo que la pregunta tenga $K$ opciones de respuesta, Siette utilizará un conjunto de $(K+1)$ curvas carectaristicas para cada uno de estos tres temas y subtemas. Dependiendo de la respuesta seleccionada el nivel de conocimiento del alumno se estimará como el producto normalizado de la estimación anterior por la curva característica de la respuesta asociada.
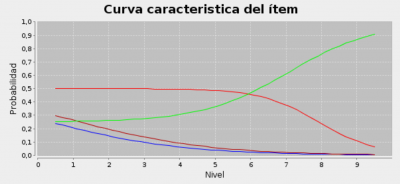
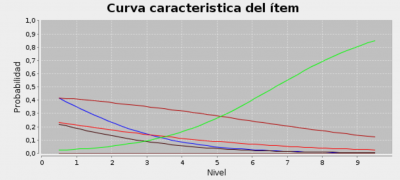
El siguiente gráfico muestra las curvas características de una pregunta de opción múltiple y respuesta única para un tema concreto. La curva verde corresponde a la respuesta correcta, las rojas a los distractores y la azul a la respuesta en blanco
Ahora bien, determinar las curvas características no es tarea fácil. La imagen anterior corresponde a una estimación empírica de las curvas características a partir de la información obtenida de los resultados de las sesiones. Sobre la distribución de frecuencias de respuesta a la pregunta para cada nivel de conocimiento se ha obtenido una curva característica mediaante interpolación, es decir, para cada nivel de conocimiento (que se obtiene por el resultado del test) se halla el porcentaje de alumnos que han seleccionado esa opción, asi se obtiene una nuvbe de puntos que se interpola mediante una función logístcia. Simplificando, éste sería el primer paso del proceso de calibración basado en el algoritmo EM (Expectantion-Maximization), que se completaría con un proceso iterativo calculando a continuación los nuevos niveles de conocimiento y volviendo a iterar hasta alcanzar un valor estable.
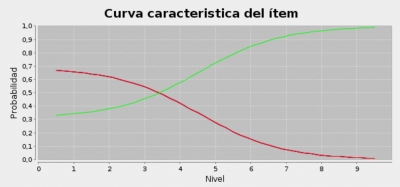
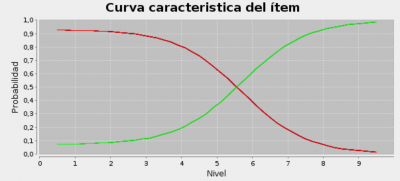
Por otra parte, muchos de los sistemas de calibración existentes utilizan sólo respuestas dicotómicas, es decir, calibran solo una curva característica para la respuesta correcta y otra para el resto de las respuestas, incluida la respuesta en blanco. Si bien es un proceso menos fino que el anterior, en la práctica es mas operativo porque no requieren tantos datos para realizar la calibración. En el caso anterior, tras aplicar un proceso de calibración estandar se obtuvieron las siguientes curvas:
En donde la curva verde corresponde a la respuesta correcta y la que aparece en rojo es la superposición de todas las demas, que al ser la misma no se muestran en la imagen.
Preguntas de respuesta múltiple independiente
En las preguntas de respuesta múltiple se plantean al alumno varias opciones de respuesta de las que debe señalar aquellas que considere correctas. Para cada opción de respuesta solo hay dos posibles acciones o marcarla o no marcarla, ya que el interfaz de respuesta no permte dejar este tipo de preguntas sin responder. No marcar ninguna opción es en si mimo una elección, al igual que marcar todas las opciones. Es importante señalar que las opciones de respuesta se consideran INDEPENDIENTES, es decir, seleccionar una opción una no condiciona seleccionar ninguna otra.
Cada una de las opciones se corrige ademas como correcta o incorrecta si se correspnde con la marca que ha establecido el profesor. Es igualmente correcto marcar una opción que el profesor ha marcado como Correcta, que no marcar una opción que el profesor ha marcado como Incorrecta (es decir, que no ha marcado como Correcta), y viceversa.
Evaluación Porcentual
La respuesta es correcta si se ha seleccionado todas las opciones marcadas como Correcta y ninguna de las marcadas como Incorrecta. Esta decisión implica que las preguntas de múltiple respuesta tengan pocas probabilidades de ser respondidas correctamente como fruto del azar, ya que para $K$ opciones, la probabilidad de acierto al azar es solo de $1/2^K$, por ejemplo para $K=4$ seria de $1/16 = 0.0625$, un 6,25%.
Evaluación Por puntos
Al evaluar esta pregunta por puntos, lo que se hace es evaluar cada una de las opciones por separado, asignándole una puntuación positiva de $1/K$ si la respuesta es acertada y de $-1/K$ si no lo es, siendo $K$ el número de opciones. La puntuación total se obtiene sumando los valores de todas las opciones.
Por ejemplo, supongamos la siguiente pregunta de respuesta múltiple, y una respuesta del alumno:
| Correcta | Marcada | Puntuación positiva | Puntuación negativa | |
|---|---|---|---|---|
| Señala los coloes de la bandera de Francia | ||||
| Rojo | Si | Si | +0.20 | |
| Azul | Si | Si | +0.20 | |
| Blanco | Si | No | -0.20 | |
| Verde | No | No | +0.20 | |
| Amarillo | No | Si | -0.20 | |
A la vista de los resultados la puntuación obtenida en esta pregunta es de +0.20 puntos.
Es importante señalar que se asume que las respuestas a cada opción son completamente INDEPENDIENTES, lo que se debe tener en cuenta al plantear la preguntas. Por ejemplo, en el caso anterior la independencia se vería alterada si el enunciado dijera “Señala los tres coloes de la bandera de Francia”, ya que condiciona al alumno a descartar algunas combinaciones.
Como opción por defecto en este tipo de preguntas la puntuación máxima positiva y la puntuacion máxima negativa valen ambas 1.0 punto, ya que si el alumno acierta todas las opciones obtendría 1.0 punto y si falla todas -1.0 punto.
Evaluación TRI
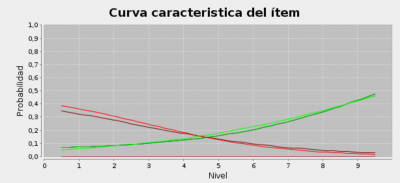
Al igual que en el caso de las preguntas de respuesta única, para este tipo de preguntas tiene mucho sentido utilizar una curva característica diferente para cada una de las opciones de respuesta. Una primera aproximación de estas curvas características obtenida de forma empírica muestra las curvas asociadas a cada opción para una pregunta con tres opciones correcta y tres incorrectas. (Véase la descripción en el epígrafe anterior).
En la práctica, si el proceso de calibracón se basa en opciones dicotómicas solo se obtendrían dos curvas, una para la respuesta con todas las opciones correctas y otra para cualquier otra combinación. Lo que suele ocurrir en estos casos es que las curvas dicotómicas que se obtiene son mucho mas discriminantes, (parámetro a), y con una menor probabilidad de acierto al azar, lo que lleva a un factor de adivinanza menor (parámetro c), ambas cualidades deseables en una curva característica.
Preguntas de respuesta libre
En el caso de las preguntas de respuesta libre, el alumno debe decidir sin ningun distractor cuál es la respuesta a la pregunta. Aunque son mas difíciles de corregir, y por tanto pueden estar sometidas a mas errores, este tipo de preguntas son las mas adecuadas para una buena evaluación. Por otra parte, dado que Siette permite revisar los patrones de respuesta y volver a corregir, los inconvenientes desde el punto de vista de la evaluación son muy marginales.
Evaluación Porcentual
Las preguntas de respuesta libre pueden tener uno o mas campos de respuesta. En el caso de que haya mas de un campo la pregunta se considera como correcta si todas los campos se corresponden con un patrón de respuesta señalado como Correcto.
Evaluación Por puntos
En el caso de la evaluación por puntos, la puntuación de la pregunta se divide entre cada uno de las posibles respuestas, si es que hay varias. Si la pregunta tiene $K$ respuestas, cada una de ellas se puntúa con $1/K$ puntos en caso de que corresponda a un patrón correcto y con $0$ puntos en caso de que corresponda a un patrón incorrecto, no corresponda a ningún patrón o se haya dejado en blanco, es decir que las opciones por defecto para la puntuacion máxima positiva y la puntuacion máxima negativa son de 1.0 y 0.0 puntos respectivamente.
En este tipo de preguntas tiene algo mas de sentido modificar la puntuación por defecto, aplicando a algunas respuestas un crédito parcial, cuando la respuesta del alumno se aproxime a la respuesta correcta aunque con algún defecto menor, o incluso penalizar alguna respuesta claramente errónea. El siguiente ejemplo ilustra esta situación:
| Correcta | Puntuación positiva | Puntuación negativa | |
|---|---|---|---|
| ¿En qué año se publico por primera vez la Teoría de la Relatividad? | |||
| 1905 | Si | +1.00 | |
| #1904#1906# | Si | +0.95 | |
| #1915#1916# | Si | +0.90 | |
| #1907#1914# | No | +0.50 | |
| #0#1900# | No | -0.2 | |
| . | No | 0.0 | |
Aunque la respuesta correcta es 1905, en que Einstein publico la Teoría especial de la relatividad; se aceptan como correctas las respuestas 1904 y 1906 porque son muy aproximadas, asignándole 0.95 puntos. Las respuestas 1915, y 1916 tambien se aceptan como correctas, ya que es la fecha en la que se publico la Teoría General de la Relatividad. A esta respuesta se le asignan 0.90 puntos. Cualquier respuesta entre 1904 y 1914 se consideran incorrectas, aunque aproximadas, por lo que solo se asigna 0.5 puntos. Cualquier respuesta con una fecha anterior a 1900 se considera un error importante y se penaliza con -0.2 puntos. Cualquier otra respuesta no puntúa, pero tampoco resta puntos. En este ejemplo, la puntuación máxima positiva de la pregunta sería 1.0 puntos y la máxima negativa -0.2 puntos.
Un inconveniente de modificar el comportamiento por defecto de las preguntas es que es necesario informar al alumno del cambio de criterio de puntuación, pregunta a pregunta. Siette actualmente no lo hace, porque eso conllevaría complicar el interfaz de respuesta del alumno que quiere mantenerse simple. Además en casos como el del ejemplo anterior, es difícil presentar esta información sin dar pistas sobre la respuesta.
Evaluación TRI
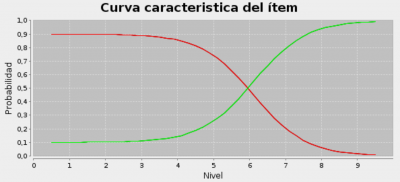
En el caso general, Siette mantiene una curva diferente para cada uno de los patrones de respuesta, uno más para el patrón genérico, es decir, la respuesta no reconocida, y otro para la respuesta en blanco. Puede haber mas de un patrón de respuesta correcto, y mas de un patrón incorrecto; por lo que al estimar las curvas características puede habrá algunas curvas ascendentes (en verde), y otras descendentes correspondientes a los patrones incorrectos (en rojo), y a la respuesta en blanco (en azul). Estas curvas pueden dar idea del nivel de conocimiento en función de cada opción de respuesta.
En este caso no es raro que solo haya un patrón de respuesta correcta, con lo que al utilizar la calibración dicotómica, la curva característica de la respuesta correcta no suele ser tan diferente al caso politómico. En general las preguntas de respuesta abierta se comportan bien, con niveles dl coeficiente de adivinanza bajos (parámetro c) ya que no admiten respuesta al azar.