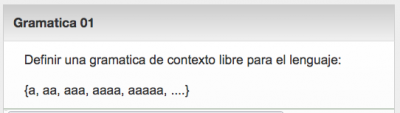
Para algunas asignaturas, tales como Teoria de Autómatas y Lenguajes Formales o Procesadores de Lenguajes, se pueden plantear preguntas cuya respuesta es una gramática de contexto libbre (o regular). Por ejemplo:

Para este tipo de problemas se ha definido un plugin que reconoce cualquier respueta dada por un alumno, sin que la gramática prpuesta deba ser identica a la propuesta, sino simplemente equivalente, es decir, que genere el mismo lenguaje.

En el ejemplo anterior la siguiente gramática sería una respuesta correcta:

A -> Aa
A -> a

Pero tambien lo seria la gramática

A -> aA
A -> a

e incluso otras gramáticas definidas mediante otros simbolos no terminales, o en otro orden tales como:

S -> a
S -> Sa

El profesor debe proporcionar una gramática que servirá como patron de comparación; sin embargo para reconocer si la respuesta de un alumno es correcta, no es suficiente por tanto una correspondencia sencilla entre el patrón y la respuesta. Es necesario comprobar mediante un procedimiento que los lenguajes generados por ambas gramaticas son equivalentes. En el caso general se ha demostrado que la equivalencia de gramáticas es una cuestión indecidible, es decir, que en el caso general no existe ningún algoritmo que nos diga si una gramática es o no equivalente a otra. Sin embargo, para los casos en llos que la gramática tiene pocas reglas, se puede resolver el problema mediante fuerza bruta. Para ello se generan todas las posibles cadenas del lenguaje a partir de la gramática de la respuesta hasta una cierta longitud y profundidad del árbol de derivaciones; y se comprueba que todas ellas están incluidas en el conjunto de cadenas generadas por la gramatica propuesta como patrón hasta con una longitud maxima y profundidad del árbol superior; y viceversa.

En caso de que las gramáticas no sean equivalentes, durante el proceso de búsqueda de la equivalencia, el plugin localiza las posibles cadenas de caracteres que diferencian a ambas gramáticas.

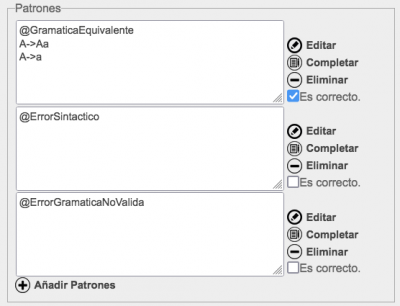
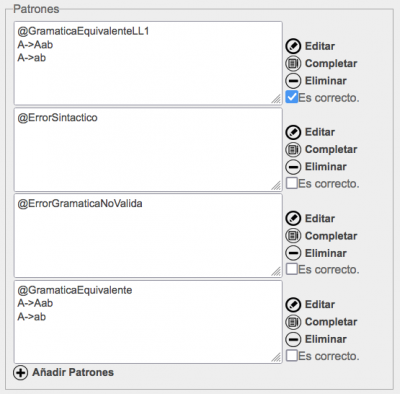
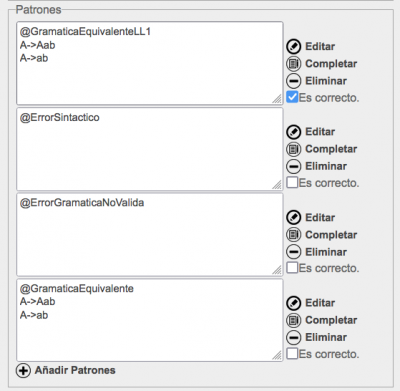
Para el ejemplo anterior, el profesor puede proporcionar varios patrones de reconocimiento:

El primer patrón se verifica cuando la gramática de la respuesta del alumno coincide con la gramática propuesta por el profesor. El segundo patrón se verifica cuando la respuesta del alumno contiene una gramática que esta mal escrita, al no seguir las reglas sintácticas para escribir gramáticas que se detallan al final de esta página. El tercer patrón corresponde a una gramática no valida, es decir, a una gramática que contiene símbolos no finalizables o simplemente no está completa. Estos dos últimos patrones sirven para informar al alumno de la causa de fallo en la corrección de su respuesta.

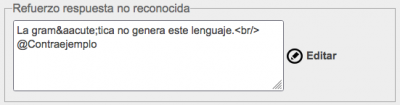
El patrón por defecto se encaja cuando no se ha podido encajar ninguno de los patrones anteriores, es decir, cuando la gramática no es equivalente, pero no tiene errores sintácticos y es una gramática correcta. En este caso, el refuerzo asociado a este patrón puede incluir un contraejemplo, es decir, una cadena que pertenece al lenguaje pero no es generada por la gramática de la respuesta o bien una cadena que no pertenece al lenguaje y es generada por la gramática de la respuesta. Para ello el refuerzo de la respuesta no reconocida se escribe:

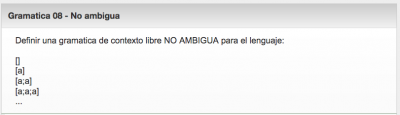
El plugin tambien puede comprobar si la gramática propuesta es o no ambigua, por ejemplo para responder a preguntas como:

En donde el conjunto de patrones ahora es:

En este caso el patrón de respuesta correcto requiere que la gramàtica solución no sea ambigua. Si lo fuera, este patrón no encajaría y se intentaría encajar con alguno de los siguientes. Suponiendo que la gramática esta bien escrita desde el punto de vista sintáctico y es correcta, si la gramática es equivalente pero ambigua, encajaría con el cuarto patrón, es decir con el patón etiquetado como @GramaticaEquivalente que ahora corresponde a un patrón incorrecto. A este patrón incorrecto se le puede asociar un refuerzo para indicar al alumno alguna de as cadenas que hacen que la gramática sea ambigua.

Finalmente, el plugin tambien permite solicitar gramáticas que cumplan la condición LL(1).

En este caso los patrones se comporta de manera similar al caso de las gramáticas ambiguas.

Nótese que no es necesario incluir el patrón de @GramaticaEquivalenteNoAmbigua, (aunque se podría incluir), ya que toda gramática LL1 tiene que ser no ambigua. Nótese también que no es ni siquiera necesario proporcionar una gramática LL(1) como patrón, ya que el plugin se encarga de verificar que la gramática de la respuesta es equivalente a la gramática del patrón y que además cumple la condición LL(1). Sin embargo si habrá que proporcionar una gramática LL(1) como ejemplo.

En el plugin de los patrones de gramáticas no es necesario repetir la gramática en cada uno de los patrones, basta con incluir la gramática en el primero de ellos. Por otra parte, los controles de ignorar mayusculas y minúsculas, espacios en blanco, etc. no son operativos.

Tanto para proporcionar el patrón como la respuesta del alumno, se deben seguir unas normas sintácticas para expresar la gramática de contexto libre. Solo es necesario proporcionar el conjunto de reglas. Los símbolos no terminales se escriben mediante letras mayusculas de la A a la Z (excluyendo la Ñ), o bien letras mayusculas seguidas de un apóstrofe, tales como A' , B' … Z', que funcionan como no terminales distintos. El primer símbolo no-terminal se tomará como axioma de la gramática.

Los símbolos terminales corresponden a letras minúsculas de la a a la z, o bien cualquier otro caracter Ascii excluyendo las letras mayusculas, los apóstrofos, comillas y el caracter $ que tiene un significado especial. No es necesario proporcionar una gramática ampliada, pero si se hace, debe usarse el símbolo $ como símbolo terminados de cadenas.

Las reglas se escriben cada una en un línea, separando el antecedente del consecuente mediante una fecha construida mediante los caracteres →. Los espacios en blanco no son significativos. La cadena vacía <html>&epsilon;</html> se puede escribir mediante la palabra reservada EPSILON, o bien dejando el consecuente vacío.

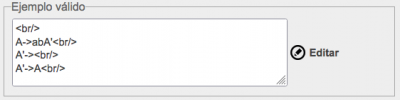
El siguiente es un ejemplo de gramática válido

 A -> [B]
 B -> aB'
 B ->
 B'-> ;aB'
 B'->